Robustness of dynamic systems
Investigators: Hana Krakovská
Stability is one of the most important concepts in dynamical systems. Local stability is a classical and well-studied concept, while defining and determining the “global” stability (robustness) of a nonlinear system is quite challenging. Over the past few decades, many different approaches have been developed to address this problem, primarily motivated by applied problems. However, the concept of resilience currently has a number of mutually inconsistent definitions. The work [1] therefore presents a comprehensive, systematic review of resilience indicators in the context of continuous dynamical systems, as well as their generalization and categorization according to mathematical properties. These steps are important to ensure more reliable, quantitatively comparable and reproducible research on resilience in dynamical systems. The above indicators are also compared in the paper within the framework of a classical model from population dynamics.
The thesis was written as a continuation of the collaboration on Hanna Krakowska’s master thesis project with supervisors Christian Kuehn and Iacopo P. Long from the Faculty of Mathematics, Technical University of Munich.
The publication also led to two invited lectures this year [2], [3].
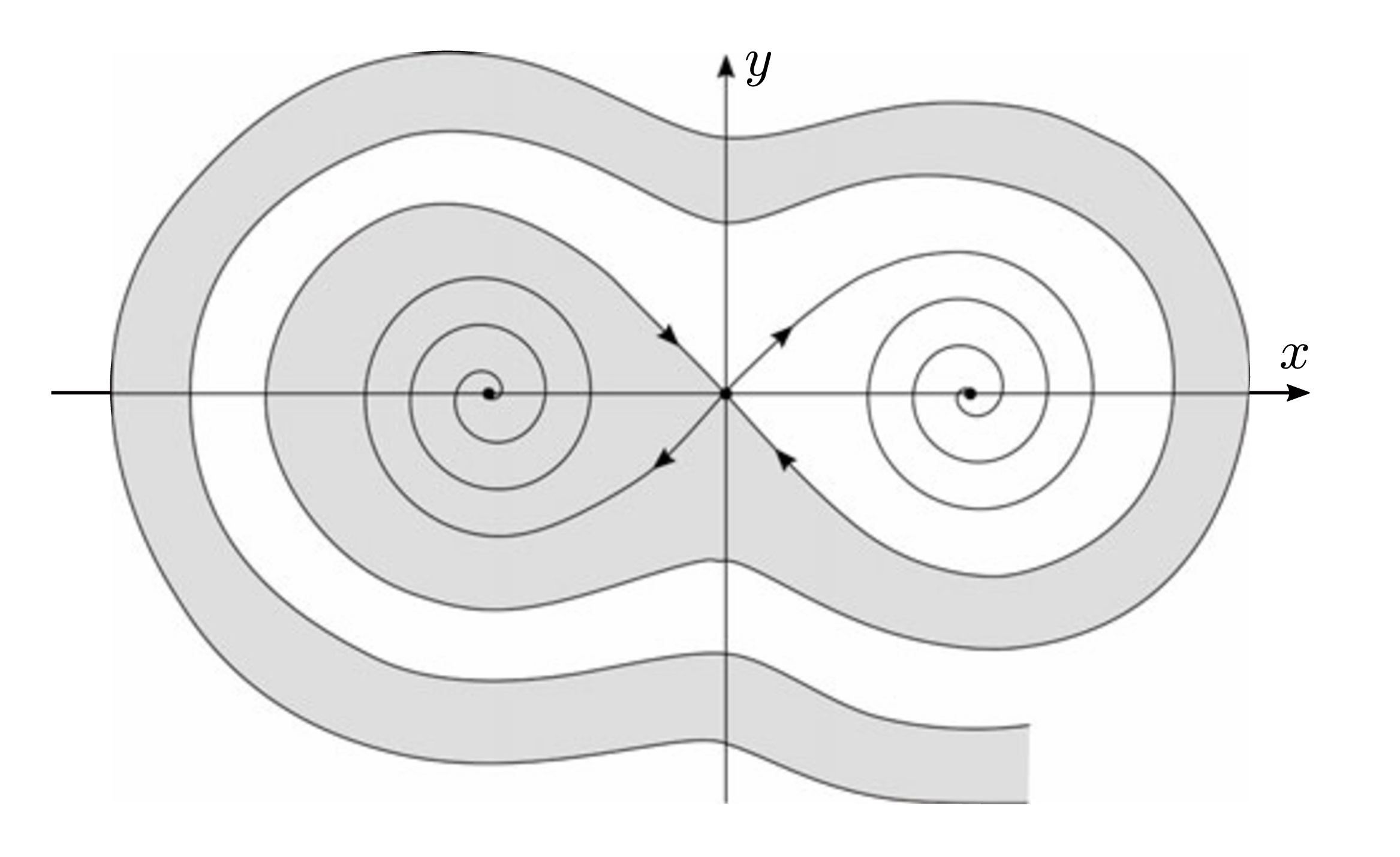
Fig.: A simple example of a stability analysis result. The unexcited Duffing oscillator represents a system with three equilibria, a saddle point and two fixed points. The fixed points are asymptotically stable and the boundary of the region of attraction of each of them is determined by the stable variety of the saddle point.
Foreign partner:
- Fakulta matematiky Technickej univerzity Mníchov
Related projects:
- VEGA č. 2/0023/22
Related publications and invited lectures:
- KRAKOVSKÁ, Hana – KUEHN, C. – LONGO, I.P. Resilience of dynamical systems. In European Journal of Applied Mathematics, 2024, vol. 35, no. 1, p. 155-200. (2023: 2.3 – IF, Q1 – JCR, 0.845 – SJR, Q2 – SJR). ISSN 0956-7925. Dostupné na: https://doi.org/10.1017/S0956792523000141 (VEGA č. 2/0023/22: Causal analysis of measured signals and time series) Typ: ADMA
- KRAKOVSKÁ, Hana. Resilience Indicators in Dynamical Systems. Lecture, invited by George Datseris (University of Exeter), Minisymposium on Multistability and global stability analysis, Conference Dynamics Days Europe, Bremen, July 29 – August 2, 2024
- KRAKOVSKÁ, Hana. Resilience of attractors in dynamical systems. Lecture, invited by Pavol Bokes (FMFI UK, Bratislava), Seminar on the Qualitative Theory of Differential Equations, October 24, 2024
 Contacts
Contacts Intranet
Intranet SK
SK