Advances in numerical methods and algorithms for the computation of complex probability distributions in uncertainty analysis of measurement results
Investigators: Viktor WITKOVSKÝ, Laura HAJZOKOVÁ , IMS SAS + foreign partners
In 2023, our collaboration with researchers from the University of Montenegro contributed to advances in probabilistic modelling and numerical methods and algorithms for the computation of complex probability distributions, which are often encountered in the analysis of uncertainties in measurement results in various application areas. The first result presents a numerical algorithm for computing a joint probability distribution that can be specified using a bivariate characteristic function, allowing practical applications for combining bivariate probability distributions and colula functions for dependence modeling. The second result focuses on a specific and substantively very broad class of probability distributions suitable for modeling many seemingly disparate physical but also biological processes, known as the Tsallis q-Gaussian distribution. We have derived the explicit form of the characteristic function of this distribution for different parameter domains and implemented a numerical algorithm for the numerical inversion of the convolution or linear combination of such distributions. From the perspective of measurement and metrology, this result has important implications for modeling sources of uncertainty in measurements, as well as for computing probability distributions characterizing the combined uncertainty of measurement results as a more accurate alternative to Monte Carlo methods. The third result is devoted to comparing the effectiveness of selected methods for numerical inversion of Laplace transforms, comparing different methods and demonstrating their effectiveness in efficiently evaluating probability densities and cumulative distribution functions.
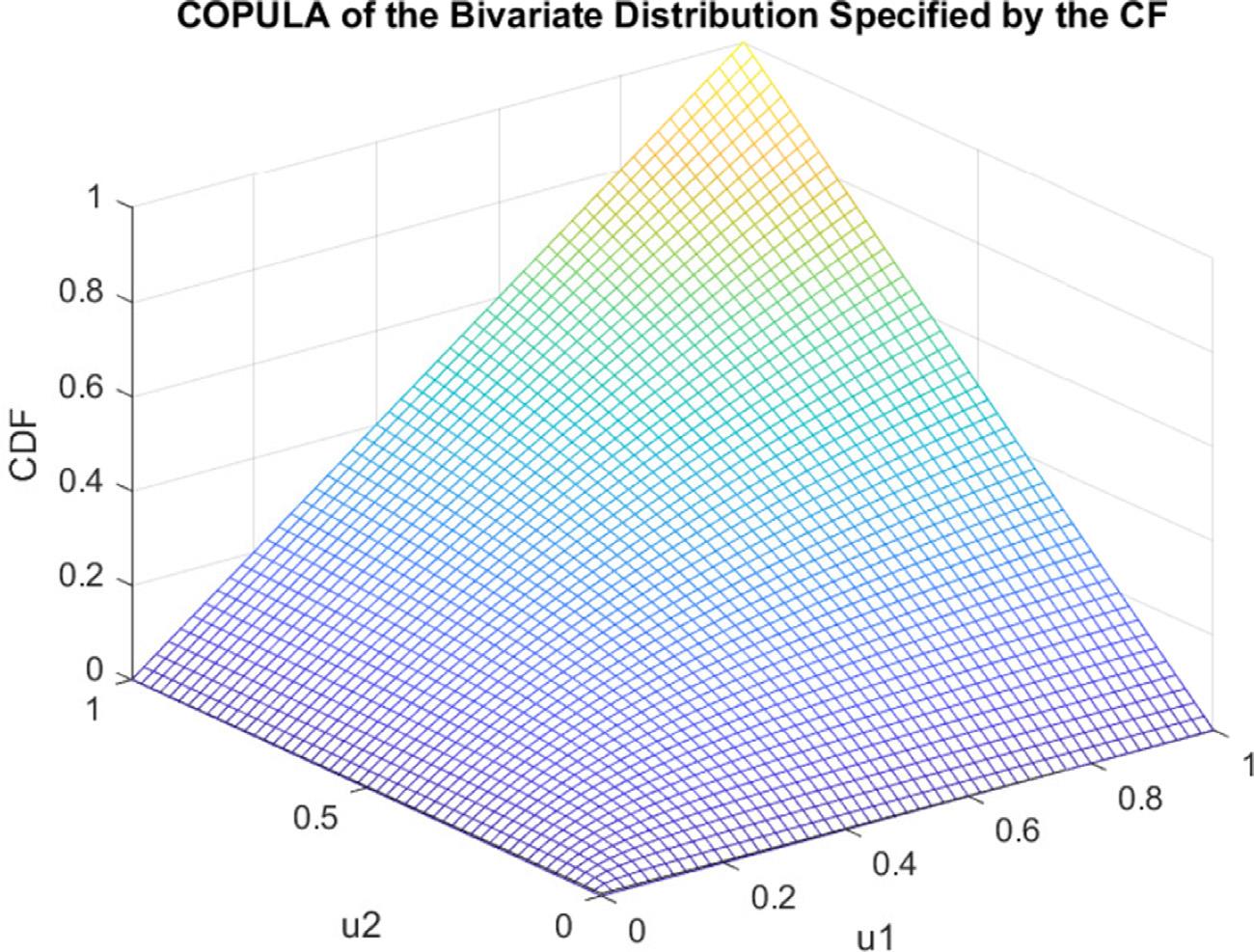
Fig. 1. The copula of the bivariate logistic distribution, which was specified by a characteristic function with parameters m = [1 , 3] and σ = [0 . 1 , 0 . 3] .
Foreign partner
- Faculty of Natural Sciences and Mathematics, University of Montenegro, Montenegro
Related projects
- APVV-21-0216 : Advanced mathematical and statistical methods for measurement and metrology.
- VEGA No. 2/0096/21 : Probability distributions and their applications in modelling and testing.
- VEGA No. 2/0023/22 : Causal analysis of measured signals and time series
Related publications:
- MIJANOVIĆ, A.** – POPOVIĆ, B.V. – WITKOVSKÝ, Viktor. A numerical inversion of the bivariate characteristic function. In Applied Mathematics and Computation, 2023, vol. 443, art. no. 127807. (2022: 4 – IF, Q1 – JCR, 0.962 – SJR, Q1 – SJR). ISSN 0096-3003. https://doi.org/10.1016/j.amc.2022.127807 (APVV-21-0216 : Advanced mathematical and statistical methods for measurement and metrology. VEGA 2/0096/21 : Probability distributions and their applications in modelling and testing. VEGA 2/0023/22 : Causal analysis of measured signals and time series) Type: ADCA
- WITKOVSKÝ, Viktor. Characteristic function of the Tsallis q-Gaussian and its applications in measurement and metrology. In Metrology, 2023, vol. 3, no. 2, p. 222-236. ISSN 2673-8244. https://doi.org/10.3390/metrology3020012 (APVV-21-0216 : Advanced mathematical and statistical methods for measurement and metrology. VEGA 2/0096/21 : Probability distributions and their applications in modelling and testing. VEGA 2/0023/22 : Causal analysis of measured signals and time series) Type: ADEB
- HAJZOKOVÁ, Laura** – WITKOVSKÝ, Viktor. Method comparison for numerical inversion of Laplace transform. In Proceedings of the 14th International Conference on Measurement. 1. vyd. – Bratislava : Institute of Measurement Science, SAS, 2023, 2023, 51-54. ISBN 978-80-972629-7-6. https://doi.org/10.23919/MEASUREMENT59122.2023.10164330 (VEGA 2/0023/22: Causal analysis of measured signals and time series) Type: ADNB
 Contacts
Contacts Intranet
Intranet SK
SK