Problems of causal analysis of deterministic time series
Investigators: Anna Krakovská, Martina Chvosteková, Jozef Jakubík
Identifying causal relationships in measured time series is a research topic that we have been working on intensively for several years. This year we have focused on discovering causality in cases where traditional tools such as the Granger test, successful for example in autoregressive processes, are not applicable [3], [4]. This is particularly the case for processes that are well modelled as deterministic dynamical systems.
We derive a fast and simple method for estimating the fractal complexity of the systems under study, which opens up new possibilities for the study of the synchronization process and efficient causal analysis of long time measurements dominated by deterministic dynamics. We have published the proposed methodology in [1], presented it at an international conference [5], [6] and published the corresponding MatLab code in [7].
Determinism in data is also problematic in the context of the so-called first principle of causality, which is the rule that cause always precedes effect. Although one might expect that, once time series are rotated, causality detection methods simply swap cause and effect, our analysis in [2] shows that no such swap occurs in the case of deterministic series. We have explored the reasons for this apparent paradox using both numerical and theoretical methods.
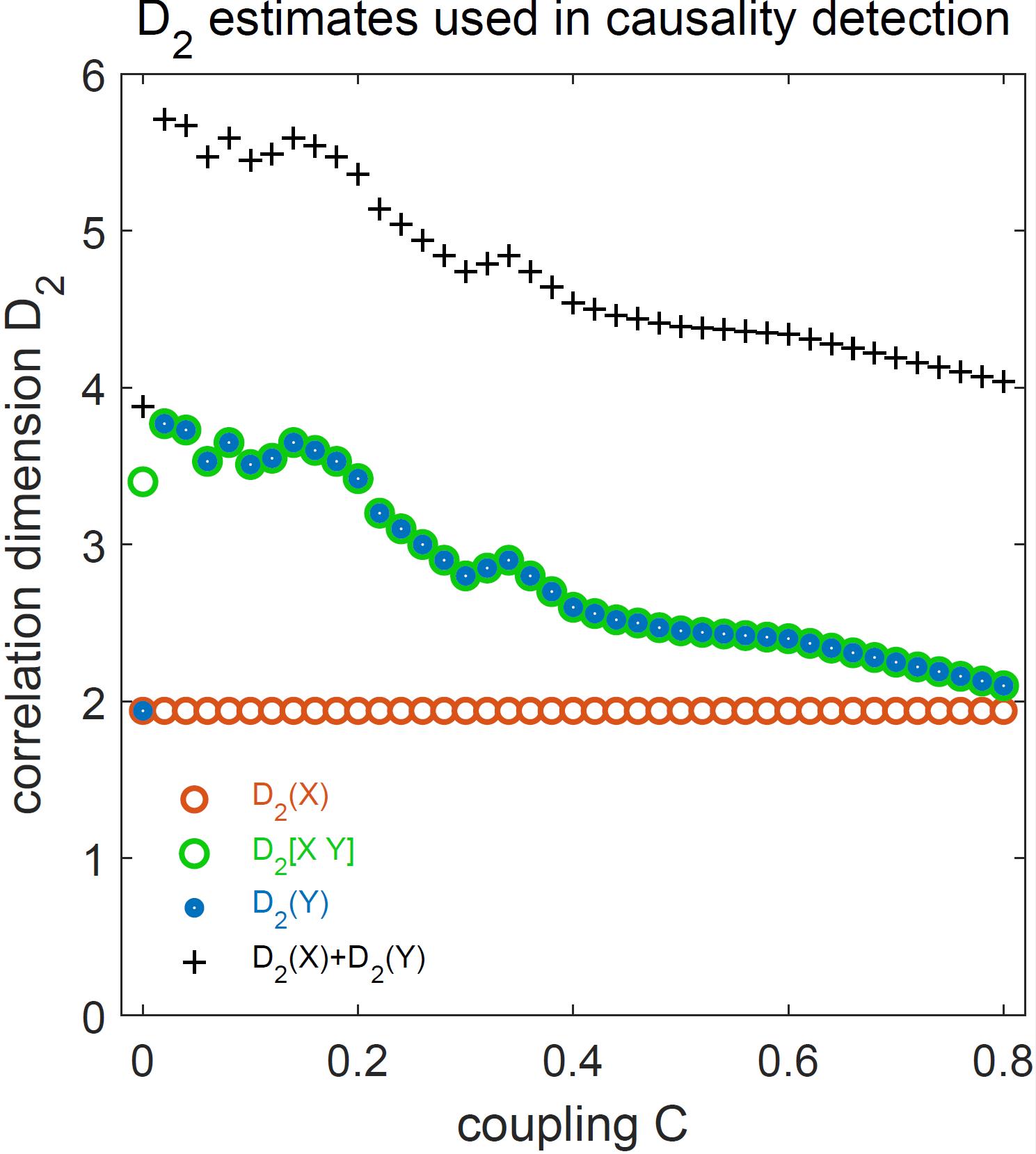
Fig. Correlation dimensions D2 of systems X, Y and their combinations for increasing strength of connection C. Comparison of the D2 estimates reliably reveals that for C>0 X causally affects Y and allows identification of the onset of synchronization.
Related projects: Addressed in the framework of projects APVV-21-0216, VEGA nr. 2/0096/21 and VEGA nr. 2/0023/22.
Publications:
- KRAKOVSKÁ, A.– CHVOSTEKOVÁ, M. Simple correlation dimension estimator and its use to detect causality. In Chaos, Solitons and Fractals, 2023, vol. 175, art. no. 113975. (2022: 7.8 – IF, Q1 – JCR, 1.393 – SJR, Q1 – SJR). ISSN 0960-0779. Dostupné na: https://doi.org/10.1016/j.chaos.2023.113975 Typ: ADCA
- JAKUBÍK, J. – PHUONG, M. – CHVOSTEKOVÁ, M. – KRAKOVSKÁ, A. Against the flow of time with multi-output models. In Measurement Science Review, 2023, vol. 23, no. 4, p. 175-183. (2022: 0.9 – IF, Q4 – JCR, 0.306 – SJR, Q3 – SJR). ISSN 1335-8871. Dostupné na: https://doi.org/10.2478/msr-2023-0023 Typ: ADDA
- CHVOSTEKOVÁ, M. Inadequacy of the Liang information flow for causal analysis. In Proceedings of the 14th International Conference on Measurement, 2023, p. 96-99. Dostupné na: https://doi.org/10.23919/MEASUREMENT59122.2023.10164449 ISBN 978-80-972629-7-6. Typ: ADNB
- CHVOSTEKOVÁ, M. A difference between an optimal parameter set for a statistical inferring of directionality of coupling for stochastic and chaotic deterministic systems based on information theory. In Proceedings of the 14th International Conference on Measurement, 2023, p. 23-26. ISBN 978-80-972629-7-6. Dostupné na: https://doi.org/10.23919/MEASUREMENT59122.2023.10164466 Typ: ADNB
- KRAKOVSKÁ, A.A two nearest neighbors estimator for Rényi dimensions and entropies, with implications for identifying causality. In Book of abstracts of Conference Dynamics Days Europe 2023, page 185, 3-8 September 2023, Naples, Italy. Dostupné na: https://sites.google.com/view/dynamicsdayseurope2023/book-of-abstracts
- JAKUBÍK, J. Non-linear smoothing of noisy chaos. In Book of abstracts of Conference Dynamics Days Europe 2023, page 187, 3-8 September 2023, Naples, Italy. Dostupné na: https://sites.google.com/view/dynamicsdayseurope2023/book-of-abstract
- KRAKOVSKÁ, A. SimpleCorrelationDimension. MATLAB Central File Exchange. https://www.mathworks.com/matlabcentral/fileexchange/136419-simplecorrelationdimension?s_tid=srchtitle_site_search_1_simpleCorrelationdimension Retrieved Oct. 10 2023.
 Contacts
Contacts Intranet
Intranet SK
SK