Volume graphics represents a set of techniques aimed at modeling, manipulation and rendering of geometric objects, which have proven to be, in many aspects, superior to traditional computer graphics approaches. The basic idea resides in the representation of a geometric object by means of 3D raster of elementary volume primitives - voxels. This data structure is the same as that of scanned real objects and thus enables simultaneous handling and rendering of synthesized and real objects.
The main advantages of volume graphics are:
Two drawbacks of volume graphics techniques are their high memory and processing time demands. However, due to the progress in both computers and specialized volume rendering hardware, these drawbacks are gradually losing their significance.
To be represented by the voxel raster, an object has to be subjected to a process called voxelization or 3D scan conversion. This is essentially a sampling process, and therefore sampling theory rules should be taken into account. The voxelization techniques implement digitization and quantization of a continuous signal, while the rendering can be described as resampling - reconstruction of a continuous signal with subsequent sampling and projection. Although both the voxelization and rendering phases are relatively independent, the quality of the rendered image can be improved by mutual adjustment of both the smoothing filter of the voxelization and reconstruction filter in the rendering.
The goal of this document is to show results of several experiments, published in details in the paper Object Voxelization by Filtering , and to propose some simple rules, which should be followed in order to voxelize objects with high possible rendering quality.The following results were obtained by voxelization and subsequent rendering of a sphere with diameter 51.2 voxel units (VU), using three different voxelization filters: Cone, Gaussian and Oriented Box Filter. Additional information concerning the filters can be found in the full version of the paper.
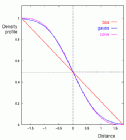
Simulated surface area density profiles for the sphere with radius 51.2, voxelized by the filters used in the experiment: cone: Cone filter, with support radius 1.8; gauss: Gaussian filter with sigma = 0.8 and neglected surface curvature; box: Oriented Box filter with halfwidth 1.8.
In order to learn more about the filter properties, the voxelized data sets were rendered by ray tracing in two configurations:
The intersection point p of a ray with the continuous surface was defined by trilinear interpolation of 8 surrounding samples and thresholding at density level 0.5. Then, for all 8 samples a normal vector was estimated and the obtained normals were interpolated for the point p by trilinear interpolation again. The interpolated surface point and normal vector were used either for shading in the case of animated sequences, or for the error estimation.
Mean error values and their standard deviations for all three voxelization filters are summarized in Table 1.
| Normal Vector Error [degree] | Surface Position Error [VU] | |||
|---|---|---|---|---|
| mean | st. dev. | mean | st. dev. | |
| Cone | 2.21 | 0.96 | -0.013 | 0.014 |
| Gaussian | 2.36 | 1.03 | -0.0038 | 0.0149 |
| Oriented Box | 0.014 | 0.020 | -0.0032 | 0.0009 |
A 3D Cone filter has spherical support with weight falling linearly from the center to the boundary. For each voxel of the grid, a normalized weighed sum of the filter with the sphere was computed. We took into account local curvature of the sphere; no approximations were done.
If the central differences technique is used for gradient estimation, it results into significant normal error.
This figure shows the surface normal error as a function of sphere parameterization. A pixel value represents angle between exact and estimated normals in degrees, multiplied by factor 50.
This animated sequence shows influence of the imprecise normal estimation on the sphere appearance. Notice "floating" of the highlight.
By taking the weighed sum, the filter blurs the object, which causes
the estimated surface point to be shifted towards the sphere center.
In spite of the fact that we used a large sphere having low surface curvature,
surface position error with approximately 3 times larger mean value
was obtained in comparison to the other filters (Gaussian, Oriented Box)
which neglected
the surface curvature (Table 1, 4-th column).
This kind of error further increases with increasing surface curvature
(i.e., smaller sphere radius).
Ray-surface intersection error estimation as a function of sphere parameterization. A pixel value represents distance between exact and estimated surface point in voxel units, multiplied by factor 2000. Value 128 represents no error, negative error is represented by values lower than 128.
A 3D Gaussian filter has also spherical symmetry as the cone filter, with bell curve weight profile. In this case, we neglected the sphere surface curvature and we treated it as planar. Thus, the density depends only on distance from the surface and its profile is nonlinear (it is defined by the sinc function).
Since the surface density profile of the Gaussian filter was similar to that of the Cone filter, both the Gaussian's and Cone's normal error images and animated sequences were very similar.
Surface normal error as a function of sphere parameterization.
Animated sequence. Notice "floating" of the highlight.
As opposite to the Cone filter, our Gaussian filter neglects the local surface curvature. As no object blurring takes place, ray-surface intersection point is estimated with lower mean error. However, its deviation is significantly larger than for the Oriented Box filter, which is caused by the fact that we reconstructed a nonlinear profile by a linear filter (see Table 1, 5-th column).
Ray-surface intersection error estimation as a function of sphere parameterization.
An Oriented Box filter is approximation of the Gaussian filter resulting in a piecewise linear profile in the surface vicinity.
We have shown in the paper that in this case the central differences gradient estimator gives surface normal with correct direction, which results in neglectible normal error and no rendering artifacts.
Surface normal error as a function of sphere parameterization.
Animated sequence. The image appears to be static, with no artifacts visible.
Similarly as our Gaussian filter, the Oriented Box filter also neglects the local surface curvature. Therefore, the ray-surface mean intersection point error is low again. However, in this case, its standard deviation is also low, which is caused by the fact, that both the voxelization (piecewise linear) filter and reconstruction filter (trilinear) are of the same order (see Table 1, 5-th column).
Ray-surface intersection error estimation as a function of sphere parameterization.
In order to minimize artifacts in visualization of voxelized objects, it is necessary to use proper combination of voxelization and reconstruction filters. We obtained the best results by a linear voxelization filter (Oriented Box filter) and linear reconstruction filters (trilinear for profile reconstruction and central differences filter for gradient estimation), which led to minimal normal vector and ray-surface intersection errors, and to artifact free renditions.
The experiments have shown that the voxelization method of choice is filtering by the oriented box filter (resulting in linear density profile in the surface area) provided that the the object details can be approximated by a sphere of a radius not smaller than 2 voxel units. The optimal radius of the filter is 1.8 and central differences should be used to compute the surface gradient. This technique should be also preferred for objects with sharp details, in spite of the fact that the volume sampling technique using the cone filter gives better results for small details (i.e., sharper edges). The latter technique has a drawback, however. Due to the nonlinear density profile introduced by the cone filter, estimation of the surface normal is charged by an error, leading to more serious artifacts (incorrect normal estimation) than slightly smoother edges.
For each sample point, the technique described in the previous section requires knowledge of its distance to the surface of the voxelized primitive. In some cases it can be computed easily (sphere, plane), and in others the object can be built by CSG operations between primitives (e.g., polyhedra by intersection of halfspaces, torus by union of many spheres).
The situation is quite different for parametric surfaces. For each sample point of the data set, its distance to the primitive has to be computed. The computation often involves solving a system of nonlinear equations. This iterative procedure is often instable and, if there are several possible solutions, the nearest one is not always obtained.
The adopted voxelization technique has the following features:
Sampling of a parametric spherical surface by binary subdivision. Samples are positioned at the centers of the quadrilaterals. For the sake of clarity, the sampling density for these pictures was set to a significantly lower value than the estimated optimum.
A Monge patch, voxelized into 256x256x256 volume. 692224 samples.
A Moebius strip, voxelized into 256x256x256 volume. 638888 samples.
Utah teapot (32 Bezier patches), voxelized into 256x256x256 volume. 586785 samples.
(Full list of publications)
|
Back to Milos Sramek's home page |
|