Chessboard Distance (CD) voxel traversal algorithm

• Voxel traversal speed-up techniques
• Chessboard Distance voxel traversal
• CD traversal with anisotropic macro regions
• CD voxel traversal algorithm for rectilinear grids
• Publications

Voxel traversal speed-up techniques

Not all voxels along the ray contribute to the rendered image with the same weight. Only some of them belong to the interesting objects, while others can be traversed rapidly or can even be skipped entirely. This capability is called space-leaping and exploits some kind of coherency inherent to the object and/or image space as well as to a sequence of consecutive images.

The macro region based voxel traversal algorithms exploit the object space coherency, i.e., a tendency of object (background) voxels to occupy connected regions of space. In this case, background voxels are gathered into cubic, parallelepipedal or spherical macro regions, which can be skipped at one step thus reducing the number of steps and therefore also the total rendering time. Various schemes for the macro region definition are possible. Some of them are based on hierarchical encoding of the scene space, others define the macro regions directly for the original voxel scene.

• Basic idea: Exploit object space coherency for speed-up:
  • Macro-regions in background area
  • Fast skipping of the whole macro-region (preferably by a single step)
• Hierarchical scene coding:
  • Macro-regions are represented as empty leaves of an oct-tree structure
  • Complex traversal of the hierarchical structure (vertical and horizontal steps)
  • Macro-regions cannot have arbitrary size and position
• Distance based techniques:
  • To each background voxel one macro-region is assigned
  • Macro-region size: approximation of the Euclidean distance of the background voxel to the nearest object voxel (city block, chessboard and chamfer distance)
  • Macro-region shape: approximation of a sphere (octahedron, cube)
  • Macro-region is defined by a single number, which can be stored in the place of the originally empty background voxel (Figure 1)
  • Simple traversal algorithms

Figure 1: Segmented CT slice of a head with assigned distances.

• Known distance based techniques:
  1. RADC: Ray Acceleration by Distance Coding Zuiderveld et al. 1992
     • DDA ray generator, various types of distances possible
  2. Proximity clouds Cohen and Sheffer 1994
     • DDA ray generator, in object vicinity switched to 6-connected ray generator due to precision, various types of distances
  3. Chessboard distance voxel traversal Sramek 1993

Chessboard Distance voxel traversal

The CD voxel traversal is based on the assumption that the chessboard distance to the nearest object voxel is assigned to each 0-voxel . Thus a cubic macro region is created around each 0-voxel:

with its center in and with side size 2n+1. In other words, the macro region represents a sphere in metrics with diameter n. Since CD is independent of the projection parameters, it can be calculated and assigned during a preprocessing phase just after the segmentation. No extra space is necessary for storage of the distance information, if we use the originally ``empty'' background voxels. In this case, in order to distinguish between the object identifier and the distance, a flag bit should be reserved within each voxel descriptor.

• Brief characteristics:
  1. Based on cubic macro-regions defined by the chessboard distance
  2. Generates a sequence of voxels (Figure 2), which are 6-connected in object vicinity (no object voxels are missed)
  3. Generates a sequence of samples at voxel faces (advantage in ray-surface intersection computation and sample compositing)
  4. Further speed-up by direction dependent macro-regions: voxel is situated in the corner of a non-symmetric macro-region (6 different distance scenes necessary)
  5. Extension for rectilinear grids is possible.
  6. Implementation in integer arithmetics
  7. The idea of CD macro-regions can be utilized also for ray templates.
• Control variables:
  1. Voxel face type (X, Y, Z)
  2. Voxel entry point coordinates (relative to voxel vertex)

Figure 2: CD algorithm: speeding up the discrete ray traversal by cubic macro regions

CD traversal with anisotropic macro regions

Let us imagine the following situation. The ray is passing in a close vicinity of an object. The step size (and therefore also its speed) is decreasing first, then it reaches its minimum and then it is again increasing. In the last phase, the factor limiting the step size is the distance to the object already passed. This drawback can be overcome by introduction of anisotropic macro regions:

where

and

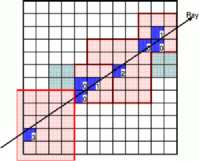
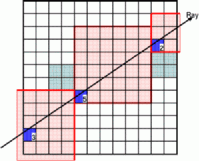
We see that in this case the actual voxel lies in one of the macro region vertices. However, instead of one symmetric macro region, 8 anisotropic macro regions can be assigned to each background voxel. Which of them is loaded to speed-up the traversal depends on the projection vector parameters. Both CD voxel traversal approaches with symmetric and anisotropic macro regions are compared in Figure 3. We see that the additional speed up is obtained by increasing the speed of the rays passing in close vicinity of objects.

(a)	(b)

Figure 3: Comparison of two CD traversal schemes with (a) isotropic and (b) anisotropic macro regions.

The anisotropic macro regions can be obtained by a minor change of the original algorithm computing the CD.

CD voxel traversal algorithm for rectilinear grids

• Motivation:
  • Tomographic data sets are often anisotropic: with higher slice density in more interesting and lower in less interesting areas.
  • Resampling to cubic voxels increases memory demands and rendering time
• Proposed solution: direct ray tracing of the rectilinear data (Figure 4).
• Grid definition:

  

  where , and is spacing along the axis .

• Algorithm features:
  1. Let be the original anisotropic grid, define a secondary grid with:
     • equal dimensions,
     • cubic voxels and
     • equal value of corresponding voxels
  2. Assign cubic macro regions to background voxels of . To each macro region in corresponds a non-cubic macro region in .
  3. Traverse exploiting real macro region size

Figure 4: Traversal of a rectilinear grid by cubic macro regions

(a)	(b)

Figure 5: Rendering of a CT data set (voxel size 0.91x0.45x0.45 mm in the lower part, 5.46x0.45x0.45 mm in the upper part). (a): correct voxel dimension, (b) voxels treated as cubic.

Selected Publications

(Full list of publications)

• Milos Sramek. Visualization of Volumetric Data by Ray Tracing ISBN 3-85403-112-2, 130 pages, Austrian Computer Society, Austria 1998 (download).
• Ivan Bajla and Milos Sramek. Nonlinear Filtering and Fast Ray Tracing of 3-D Image Data IEEE Engineering in Medicine and Biology Magazine, 2(17):73--80, 1997.
• Milos Sramek. Fast ray-tracing of rectilinear volume data; In M. Göbel, J. David, P. Slavík, and J. J. van Wijk, editors, Virtual Environments and Scientific Visualization '96, pages 201--210. Springer, New York, 1996.
• Milos Sramek. Cubic macro-regions for fast voxel traversal. Machine Graphics & Vision, 3(1/2):171--179, 1994.
• Milos Sramek. Fast surface rendering from raster data by voxel traversal using chessboard distance. In R. Daniel Bergeron and Arie E. Kaufman, editors, Visualization'94, pages 188--195, Washington, D.C., October 17--21, 1994. IEEE Computer Society Press.
• Milos Sramek. An algorithm for fast voxel scene traversal. In Václav Skala, editor, Proceedings of the Winter School on Computer Graphics and CAD systems, pages 207--220, University of West Bohemia, Plzen, Czech Republic, January 19--20, 1994.
• Igor Holländer and Milos Sramek. An Interactive Tool for Manipulation and Presentation of 3D Tomographic Data. In H. U. Lemke, K. Inamura, C. C. Jaffee, and R. Felix, editors, CAR '93 Computer Assisted Radiology, pages 278--383, Berlin, 1993. Springer-Verlag.

Back to Milos Sramek's home page